Typed [RE]

February 7, 2022 10 minute read

Flag checker made with Rust’s trait implementations and the Rust compiler.

Challenge Description

~~Haskell~~ Rust is a dynamically typed, interpreted language. Can you get my code to stop erroring?

Exploring the challenge

If we try to compile it, we indeed get compilation error.

Seems like the error is some type mismatch (or in Rust terms, the bound trait is not implemented). Ignoring (or at least trying to) the crazy names, I opened up the file, and was greeted with a greater nightmare.

I took quite a bit of time to learn Rust enough to understand what this is doing. And it appeared to me that the flag check is written with the compile-time type checking routine.

struct One<T>(PhantomData<T>);
struct Zero;

trait Add<T> {
    type Apply;
}
impl<T> Add<Zero> for T {
    type Apply = T;
}
impl<T, V> Add<One<V>> for T
where
    T: Add<V>,
{
    type Apply = One<<T as Add<V>>::Apply>;
}

I started by renaming the first trait + impl section, and realized that these traits, since they are implemented for all types, form a sort of recursion. For example, Add here can be used as <T as Add<V>>::Apply where T and V are zero or more layers of One outside of Zero (this is by looking at parts later on in the code).

The naming here seems like it is out of nowhere, because the actual analysis is not top down, but kinda all over the place. So, just stick with me here.

It is now useful to abstract an n-layered One as a single number n, so Zero would naturally be 0. Applying similar “recursion analysis” for the following few traits, we can conclude the following:

// DangGangGang -> Add
<i as Add<j>>::Apply // i + j

// DidGigGig -> Mult
<i as Mult<j>>::Apply // i * j

// DangGig -> Sub
<i as Sub<j>>::Apply // i - j

// DanceDanceGang -> Diff
<i as Diff<j>>:Apply // i != j ? 1 : 0

With this, I also renamed DanceGongGong to Ten, and DidGiceGice to Hundred

Before:

type DanceGongGong = One<One<One<One<One<One<One<One<One<One<Zero>>>>>>>>>>;
type DidGiceGice = <DanceGongGong as Mult<DanceGongGong>>::DidGong;

After:

type Ten = One<One<One<One<One<One<One<One<One<One<Zero>>>>>>>>>>;
type Hundred = <Ten as Mult<Ten>>::Apply;

What are we supposed to do?

At the very bottom of the source code, we find this:

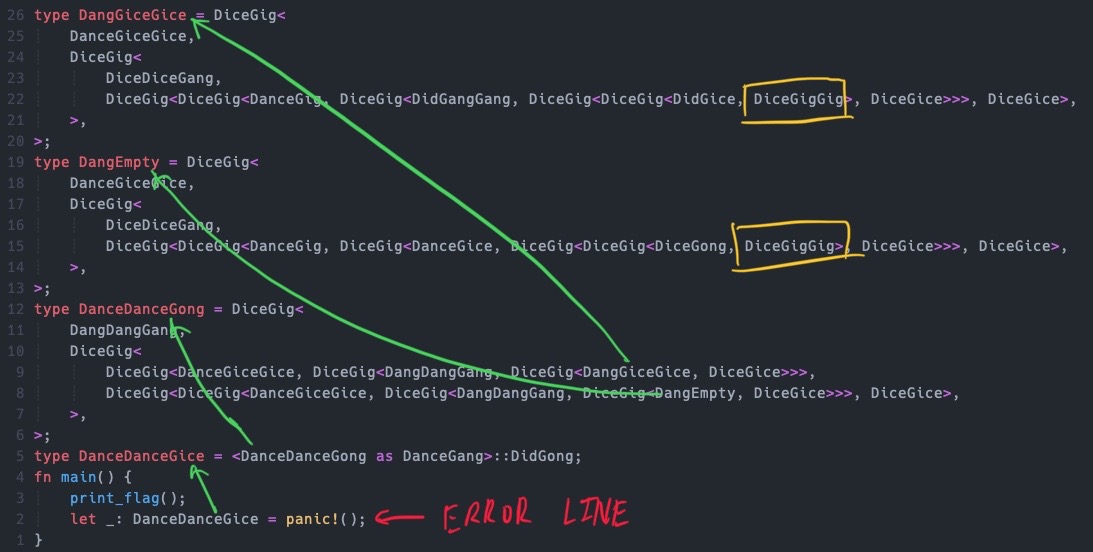
Notice the references (denoted by arrows)

I’ve boxed out (in yellow) a variable called DiceGigGig.

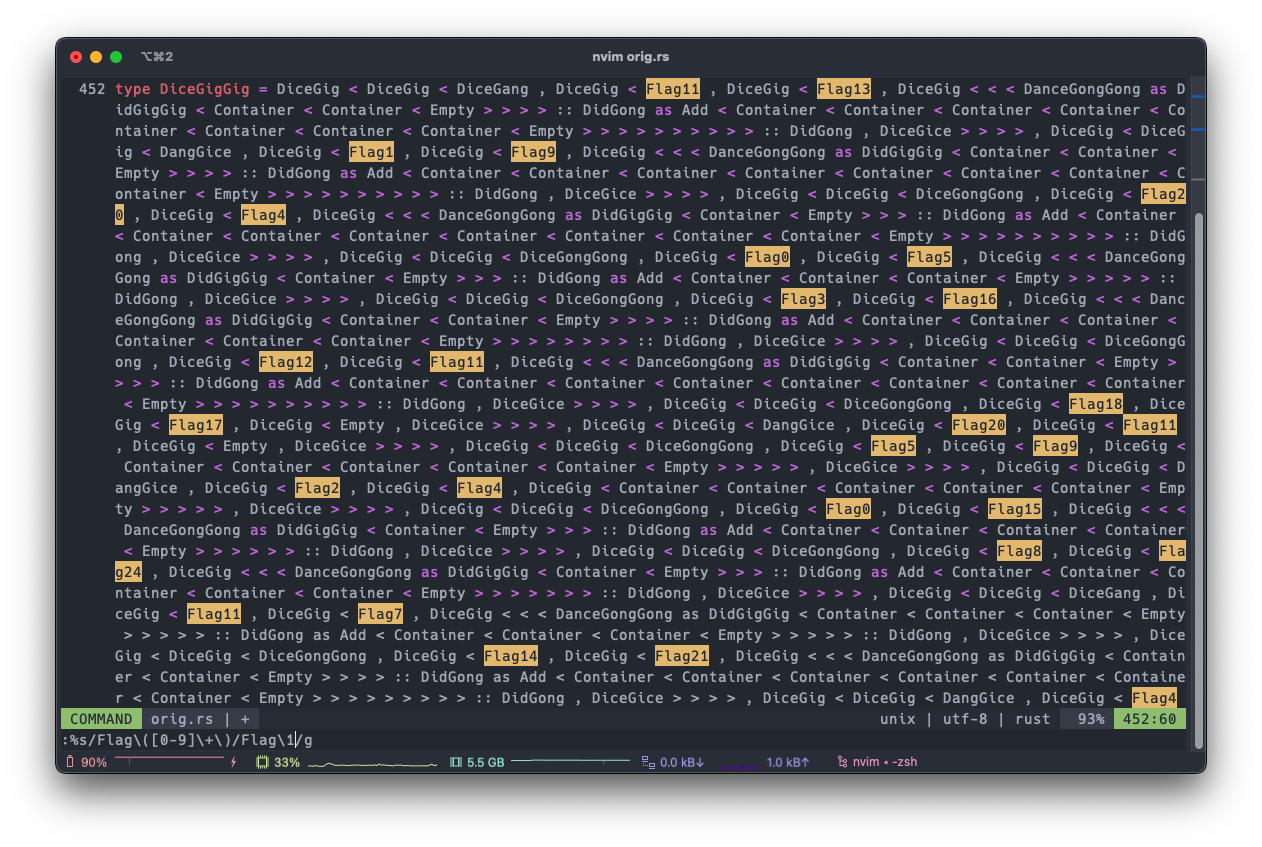
And the Flag0 to Flag24 are assigned to types Char_, Char0 to Char9, and CharA to CharZ.

And this is where I got the interpretation and naming from earlier.

So we have a sort of rough outline: we need to assign flag characters to the right character (type), and it will satisfy the type constraints. This can be confirmed by the print_flag function as well.

fn print_flag() {
	println!(
		"dice{{{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}{}}}",
		Flag0::CHAR, Flag1::CHAR, Flag2::CHAR, Flag3::CHAR, Flag4::CHAR, Flag5::CHAR, Flag6::CHAR, Flag7::CHAR, Flag8::CHAR, Flag9::CHAR, Flag10::CHAR, Flag11::CHAR, Flag12::CHAR, Flag13::CHAR, Flag14::CHAR, Flag15::CHAR, Flag16::CHAR, Flag17::CHAR, Flag18::CHAR, Flag19::CHAR, Flag20::CHAR, Flag21::CHAR, Flag22::CHAR, Flag23::CHAR, Flag24::CHAR);
}

Ok, so what do the big blocks mean?

We have to jump a little (again), to trait DanceGang. This is the fifth, and also the last, trait we need to figure out.

The repeating pattern of struct and impl (which just sets the inner type to itself) made me curious. So I gathered all the struct and renamed them. I also renamed DanceGang to Operation (stick with me!).

struct E1;
struct E2;
...
struct E13;
struct E14;

trait Operation { type Apply; }
impl Operation for E1 { type Apply = E1; }
impl Operation for E2 { type Apply = E2; }
...
impl Operation for E12 { type Apply = E12; }
impl Operation for E13 { type Apply = E13; }
impl Operation for E14 { type Apply = E14; }
impl Operation for Zero { type Apply = Zero; }
impl<T> Operation for One<T> { type Apply = One<T>; }

I also renamed DiceGice to Null and DiceGig to Pair (random? definitely :D). This is useful to understand the last round of renaming and refactoring (I promise it is the last).

You will notice that there are more impls for Operation below what I’ve shown above. I noticed that they all follow a pattern of

impl<...> Operation for Pair<E?, XXX>
where ...
{
	type Apply = ...;
}

I made a good guess that each E? denotes a unique operation done on XXX. So I reordered and grouped them for better reference.

And here, I saw things such as Pair<T, Pair<V, Null>> and Pair<T, Pair<V, W>>

Yoooo, where my LISP bois at

Mega hypothesis: The operations are functions on this data structure (I call it list, LISP calls it cons). The big blocks define operations (and their order) on a list (presumably the largest one containing the Flag?s).

We’re done with renaming stuffs, right?

After a painful amount of time reformatting the biggest block (I call it Level1, so the other 3 are obviously Level2, Level3, Level4 respectively), I realised it is a list of a pattern

Pair < Pair < E1 , Pair < Flag11 , Pair < Flag13 , Pair <
	< < Ten as Mult < One < One < Zero > > > > :: Apply as
		Add < One < One < One < One < One < One < One < One < Zero > > > > > > > > > > :: Apply ,
	Null > > > > ,

Pair < Pair < E2 , Pair < Flag1 , Pair < Flag9 , Pair < 
	< < Ten as Mult < One < One < Zero > > > > :: Apply as
		Add < One < One < One < One < One < One < One < One < Zero > > > > > > > > > > :: Apply ,
	Null > > > > ,

...

So I just refactored all of them into numbers (remember our abstraction)

Pair < Pair < E1 , Pair < Flag11 , Pair < Flag13 , Pair < 28, Null > > > > ,
Pair < Pair < E2 , Pair < Flag1 , Pair < Flag9 , Pair < 28, Null > > > > ,
Pair < Pair < E3 , Pair < Flag20 , Pair < Flag4 , Pair < 18 , Null > > > > ,
...

For the sake of simplicity, I will write an Operation of E? on List as $Op_{?}(List)$, else $Op(X) := Op_{a}(b) \text{ if X = [a, b], else } X$

We’re now gonna study the behavior of the various operations. Using the knowledge of data types and recursions, this should be quite ok to do (especially after the hard work of renaming).

\[\begin{align*} Op_1 &:= map(Add, list)\\ Op_2 &:= map(Mult, list)\\ Op_3 &:= map(Sub, list)\\ Op_4 &:= \text{apply } Op(\text{last element})\\ Op_6 &:= \text{return } Op(\text{last element})\\ Op_9 &:= Op_{\text{first element}}(\text{rest of the list})\\ Op_{13} &:= \text{drop every 3rd element, starting with first}\\ Op_{14} &:= Op_{\text{first element}}(\text{second element})\\ \end{align*}\]

Using the above, and knowing we will be applying Op(Level4), I reduced it to

\[Op_9([E10, Op_{13}(Level1)])\]

Which, although probably wrong by a whole lot, I still predicted that it’s most likely dropping every 3rd constraint in Level1. Then applying a check on every constraint like:

Pair < Pair < E2 , Pair < Flag1 , Pair < Flag9 , Pair < 28, Null > > > > ,

is equivalent to checking

\[flag_1 \cdot flag_9 = 28\]

So, with a little search and replace, and some python z3 magic, we can get the flag.

Final Script

from z3 import *

flag = [BitVec(str(i), 8) for i in range(25)]
s = Solver()
alphabet = "_0123456789abcdefghijklmnopqrstuvwxyz"

s.add(flag[1] * flag[9] == 28)
s.add(flag[20] - flag[4] == 18)
s.add(flag[3] - flag[16] == 26)
s.add(flag[12] - flag[11] == 28)
s.add(flag[20] * flag[11] == 0)
s.add(flag[5] - flag[9] == 5)
s.add(flag[0] - flag[15] == 14)
s.add(flag[8] - flag[24] == 15)
s.add(flag[14] - flag[21] == 27)
s.add(flag[4] * flag[16] == 0)
s.add(flag[24] + flag[16] == 4)
s.add(flag[3] - flag[0] == 4)
s.add(flag[7] - flag[15] == 21)
s.add(flag[18] + flag[5] == 30)
s.add(flag[7] - flag[21] == 27)
s.add(flag[13] * flag[18] == 341)
s.add(flag[19] - flag[23] == 13)
s.add(flag[14] + flag[20] == 47)
s.add(flag[10] + flag[2] == 33)
s.add(flag[20] - flag[10] == 14)
s.add(flag[22] - flag[23] == 21)
s.add(flag[15] * flag[18] == 88)
s.add(flag[22] * flag[24] == 96)
s.add(flag[0] * flag[23] == 66)
s.add(flag[8] - flag[11] == 19)
s.add(flag[19] + flag[13] == 47)
s.add(flag[17] * flag[22] == 240)
s.add(flag[16] + flag[14] == 29)
s.add(flag[19] - flag[4] == 16)
s.add(flag[24] + flag[3] == 30)
s.add(flag[10] * flag[5] == 76)
s.add(flag[20] - flag[19] == 2)
s.add(flag[24] * flag[12] == 112)
s.add(flag[24] - flag[16] == 4)
s.add(flag[1] + flag[20] == 20)
s.add(flag[1] * flag[17] == 20)
s.add(flag[5] - flag[18] == 8)
s.add(flag[16] + flag[22] == 24)
s.add(flag[6] * flag[21] == 48)
s.add(flag[6] + flag[22] == 48)

if s.check() == sat:
  for ch in flag:
    print(alphabet[s.model()[ch].as_long()], end="")

  print()

Flag: dice{l1sp_insid3_rus7_9afh1n23}

David Tan