Optinimize [RE]
Reversing program wrote in nim-lang that uses the bigints library for big integer math.
Challenge Description
Nim is good at bignum arithmetic.
Playing around
If we run this program, we see that it prints out the flag character by character, but it seemingly stops after a few characters in. Later on, I learned that the flag generation routine is just too slow, so we’ll have to optimize it, unsurprisingly, given the challenge name.
$ ./main
SECCON{3b42
Investigation
Opening this up in Ghidra, we can already see functions like NimMain, NimMainInner, etc. These tells us that we are working with nim-lang. There are also many functions in the format <name>...bigints...bigints_u.... Note the <name> portion as I will call the functions just by that name.
Upon searching “nim lang bigints”, I found this library: nimlang/bigints. Looking at the BigInts type in src/bigints.nim, and refer to initBigInt in ghidra, we can create a bigint type with the correct fields. Right click the variable (param1) > “Auto Create Structure” > right click again > “Edit Data Type”.
There are multiple
initBigIntfunctions, mine uses.._u208but either one can be used to create the custom type.
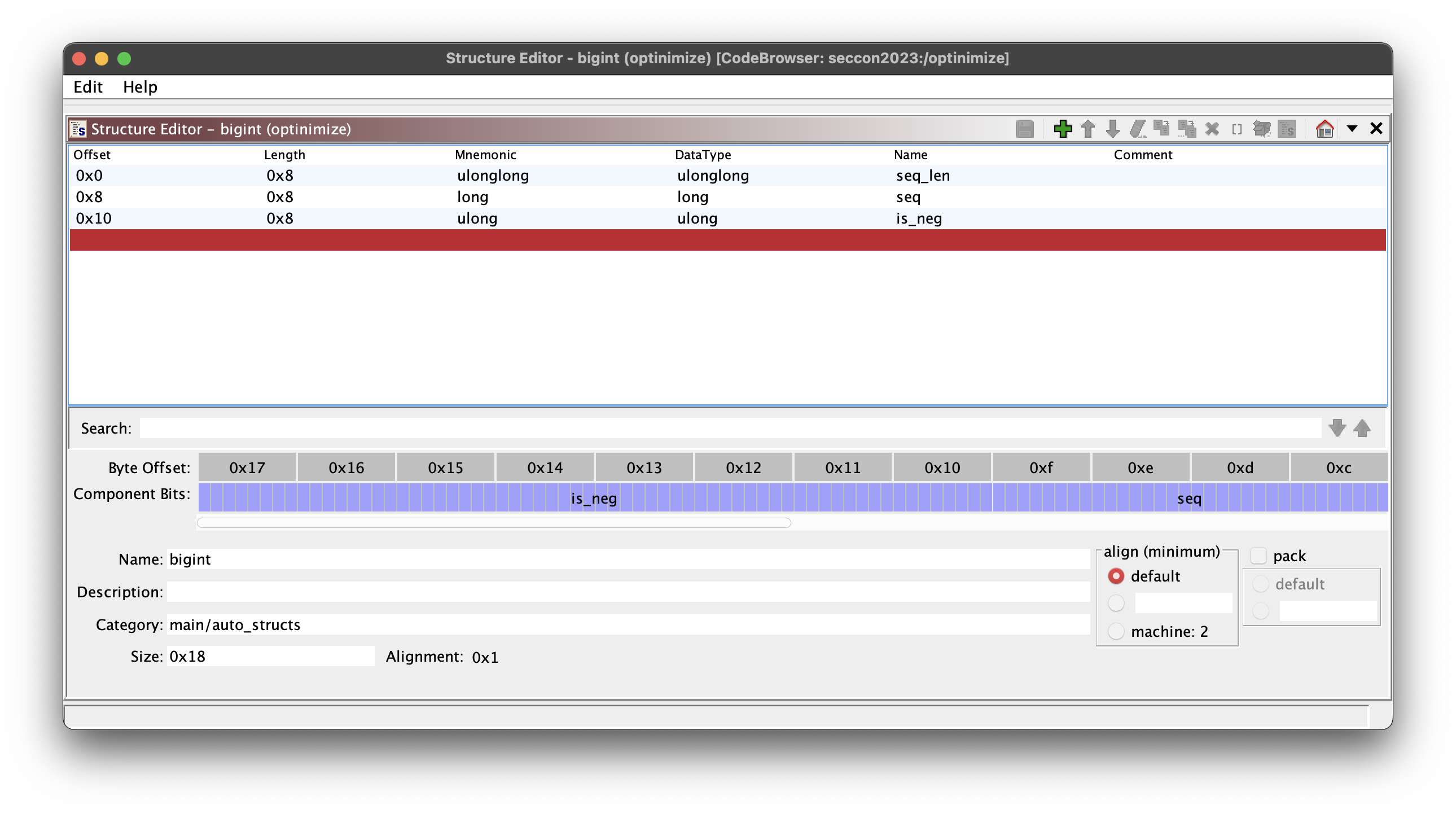
The mappings should be easy to figure out from the code + knowledge from the library source code we found earlier.
Understanding the binary
If we look at main (NimMainModule), we can retype some variables with our new bigint type, and Ghidra will give us better decompilations. For example:
void NimMainModule(void)
{
...
do {
_DAT_00118270 = 0;
...
k__main_u69 = 0;
_DAT_00118268 = 0;
...
Retyping k__main_u69 to bigint will turn this part into
void NimMainModule(void)
{
...
do {
k__main_u69.is_neg = 0;
...
k__main_u69.seq_len = 0;
k__main_u69.seq = 0;
...
Essentially, I just went around and retyping variables that were passed into initBigInt. Ignoring the details, we can see that NimMainModule loops through ns__main_u18 array and takes each element (n__main_u68), passing it into Q().
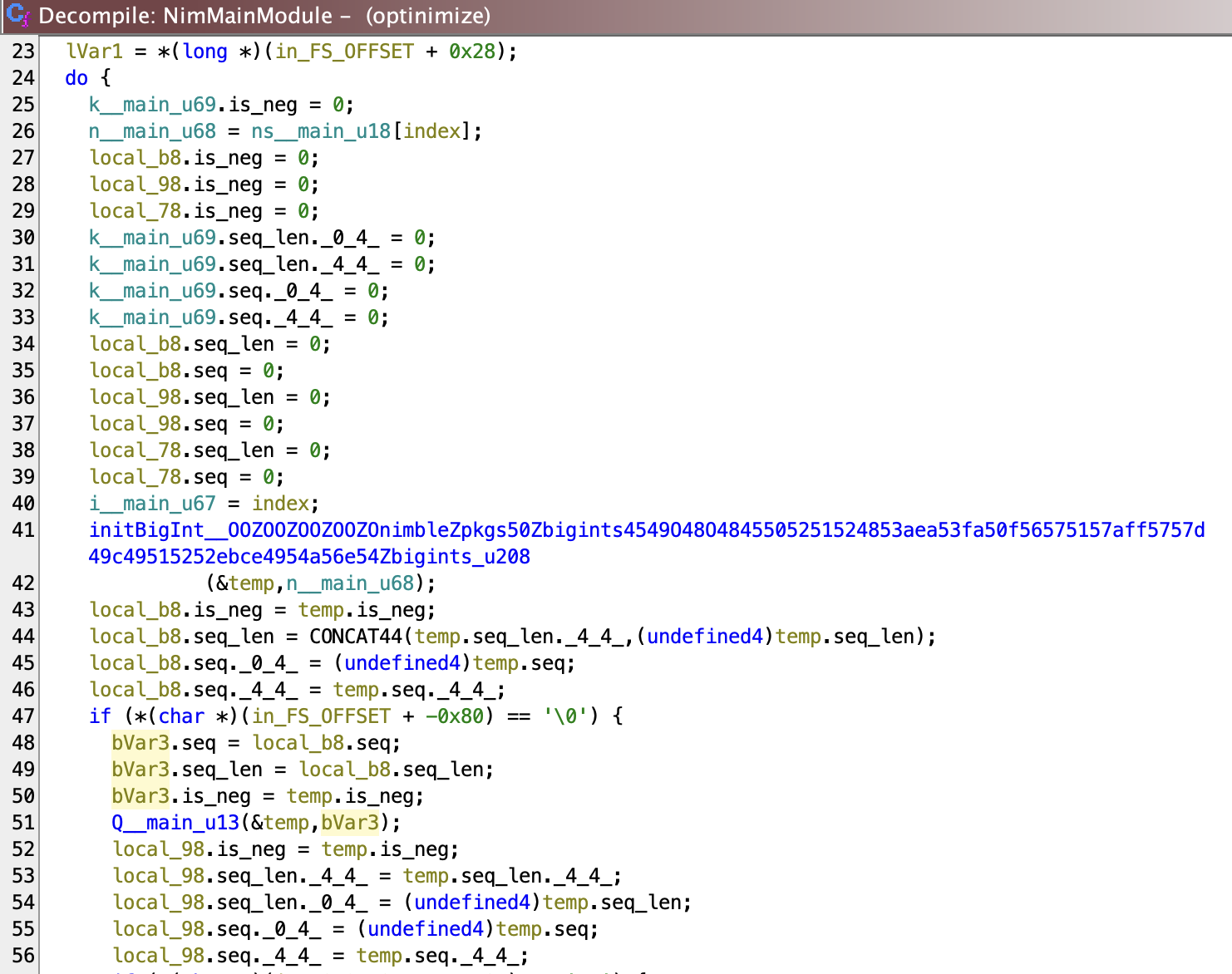
If we go into Q, we can retype and tidy up the code, and we see it calls P().
Because understanding the program statically is too hard, I rewrote the logic in python:
ns = [ 0x4a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x55, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x6f, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x79, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x80, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x95, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xae, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xbf, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xc7, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd5, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x06, 0x03, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xc8, 0x1a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xba, 0x24, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x3d, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x43, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x26, 0x56, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd9, 0x6a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x03, 0x71, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x1b, 0x90, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x03, 0x9e, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xb6, 0x5f, 0x1e, 0x00, 0x00, 0x00, 0x00, 0x00, 0x64, 0xf7, 0x26, 0x00, 0x00, 0x00, 0x00, 0x00, 0x9e, 0xbd, 0x30, 0x00, 0x00, 0x00, 0x00, 0x00, 0x78, 0x76, 0x40, 0x00, 0x00, 0x00, 0x00, 0x00, 0x3b, 0x17, 0x5b, 0x00, 0x00, 0x00, 0x00, 0x00, 0xb1, 0xe3, 0x6f, 0x00, 0x00, 0x00, 0x00, 0x00, 0x25, 0xef, 0x78, 0x00, 0x00, 0x00, 0x00, 0x00, 0x5f, 0x8e, 0x85, 0x00, 0x00, 0x00, 0x00, 0x00, 0x39, 0xc6, 0x98, 0x00, 0x00, 0x00, 0x00, 0x00, 0xf6, 0x6a, 0xad, 0x00, 0x00, 0x00, 0x00, 0x00, 0x96, 0x00, 0x08, 0x01, 0x00, 0x00, 0x00, 0x00, 0xcd, 0x08, 0x8e, 0x01, 0x00, 0x00, 0x00, 0x00, 0x07, 0x61, 0xbb, 0x01, 0x00, 0x00, 0x00, 0x00, 0xf1, 0x0f, 0xf5, 0x01, 0x00, 0x00, 0x00, 0x00, 0x27, 0x63, 0x5c, 0x02, 0x00, 0x00, 0x00, 0x00, 0xb6, 0x71, 0xa9, 0x02, 0x00, 0x00, 0x00, 0x00, 0x93, 0x84, 0xd6, 0x02, 0x00, 0x00, 0x00, 0x00, 0xc0, 0xf0, 0x62, 0x03, 0x00, 0x00, 0x00, 0x00, 0xad, 0x8e, 0x78, 0x03, 0x00, 0x00, 0x00, 0x00, 0xed, 0xa8, 0xca, 0x03, 0x00, 0x00, 0x00, 0x00 ]
cs = [ 0x3c, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xf4, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x1a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x8a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x17, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x7c, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x4c, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xdf, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x21, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xdf, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xb0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x12, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xb8, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x4e, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xfa, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd9, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x2d, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x66, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xfa, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd4, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x95, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xf0, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x66, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x6d, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xce, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x69, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x7d, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x95, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xea, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd9, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x0a, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xeb, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x27, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x63, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x75, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x11, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x37, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0xd4, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00 ]
assert(len(ns) == len(cs))
# UTIL FUNCTION
def arrconcatbytes(arr, size):
result = []
for index in range(len(arr) // size):
val = 0
for i in range(size):
val |= arr[size*index + i] << (8 * i)
result.append(val)
return result
ns = arrconcatbytes(ns, 8)
cs = arrconcatbytes(cs, 8)
print("ns[] = { %s }" % ", ".join(map(str, ns)))
print("cs[] = { %s }" % ", ".join(map(str, cs)))
def P(x):
a = 3
b = 0
c = 2
if x == 0: x = a
elif x == 1: x = b
elif x == 2: x = c
else:
# (guessed this part)
while 2 < x:
a, b, c = b, c, a + b
x -= 1
x = c
return x
def Q(x):
i, j = 0, 0
while i < x:
j += 1
if P(j) % j == 0:
i = i + 1
return j
def main():
# not exactly the same codewise, but logically equivalent
for i in range(len(ns)):
k = Q(ns[i]) % 0x100
print(chr(cs[i] ^ k), end='')
Solution
After laying the code out in python (I kind of guessed the final part in the while loop cause that part of the code barely made sense to me), I verified that it matched the output of the original program. Since I wanted to speed up the execution, it is good to know what sequence P generates, then we might be able to use some properties to speed up the loop in Q.
After running P(i) for the first few values of i (3, 0, 2, 3, 2, 5, …), I searched on OEIS and found that it generates the Perrin numbers. Q is just such that Q(x) is the x-th number n > 0, such that the n+1th Pierrin number or P(n) (P(0) is the 1st, etc.) is divisible by n.
Let’s look at an example to better illustrate: Q(4) gives 5 because 1 | P(1), 2 | P(2), 3 | P(3), 5 | P(5), so the 4th is number 5.
Quoted from wikipedia:
It has been proven that for all primes
p,pdividesP(p). However, the converse is not true: for some composite numbersn,nmay still divideP(n). Ifnhas this property, it is called a “Perrin pseudoprime”.
Since there are only a few pseudoprimes (up to a reasonably large number) already given in the wiki page, we just need a fast way to generate all the primes (up to a large enough number), insert the pseudoprimes in, and we have a precomputed list of numbers satisfying the above constraint. We will then have to only look up the array at index x, and the value is Q(x).
For prime number generation, I asked a friend for the code for wheel factorization (fast prime generation) written in C++.
Final Script
#include <bits/stdc++.h>
using namespace std;
// Wheel factorization (don't know how it works, don't care)
vector<long long> sieve(const long long N, const long long Q = 17, const long long L = 1 << 15) {
static const long long rs[] = {1, 7, 11, 13, 17, 19, 23, 29};
struct P {
P(long long p) : p(p) {}
long long p;
long long pos[8];
};
auto approx_prime_count = [](const long long N) -> long long {
return N > 60184 ? N / (log(N) - 1.1)
: max(1., N / (log(N) - 1.11)) + 1;
};
const long long v = sqrt(N), vv = sqrt(v);
vector<bool> isp(v + 1, true);
for (long long i = 2; i <= vv; ++i)
if (isp[i]) {
for (long long j = i * i; j <= v; j += i) isp[j] = false;
}
const long long rsize = approx_prime_count(N + 30);
vector<long long> primes = {2, 3, 5};
long long psize = 3;
primes.resize(rsize);
vector<P> sprimes;
size_t pbeg = 0;
long long prod = 1;
for (long long p = 7; p <= v; ++p) {
if (!isp[p]) continue;
if (p <= Q) prod *= p, ++pbeg, primes[psize++] = p;
auto pp = P(p);
for (long long t = 0; t < 8; ++t) {
long long j = (p <= Q) ? p : p * p;
while (j % 30 != rs[t]) j += p << 1;
pp.pos[t] = j / 30;
}
sprimes.push_back(pp);
}
vector<unsigned char> pre(prod, 0xFF);
for (size_t pi = 0; pi < pbeg; ++pi) {
auto pp = sprimes[pi];
const long long p = pp.p;
for (long long t = 0; t < 8; ++t) {
const unsigned char m = ~(1 << t);
for (long long i = pp.pos[t]; i < prod; i += p) pre[i] &= m;
}
}
const long long block_size = (L + prod - 1) / prod * prod;
vector<unsigned char> block(block_size);
unsigned char* pblock = block.data();
const long long M = (N + 29) / 30;
for (long long beg = 0; beg < M; beg += block_size, pblock -= block_size) {
long long end = min(M, beg + block_size);
for (long long i = beg; i < end; i += prod) {
copy(pre.begin(), pre.end(), pblock + i);
}
if (beg == 0) pblock[0] &= 0xFE;
for (size_t pi = pbeg; pi < sprimes.size(); ++pi) {
auto& pp = sprimes[pi];
const long long p = pp.p;
for (long long t = 0; t < 8; ++t) {
long long i = pp.pos[t];
const unsigned char m = ~(1 << t);
for (; i < end; i += p) pblock[i] &= m;
pp.pos[t] = i;
}
}
for (long long i = beg; i < end; ++i) {
for (long long m = pblock[i]; m > 0; m &= m - 1) {
primes[psize++] = i * 30 + rs[__builtin_ctz(m)];
}
}
}
assert(psize <= rsize);
while (psize > 0 && primes[psize - 1] > N) --psize;
primes.resize(psize);
return primes;
}
int main() {
long long ns[] = { 74, 85, 111, 121, 128, 149, 174, 191, 199, 213, 774, 6856, 9402, 15616, 17153, 22054, 27353, 28931, 36891, 40451, 1990582, 2553700, 3194270, 4224632, 5969723, 7332785, 7925541, 8752735, 10012217, 11365110, 17301654, 26085581, 29057287, 32837617, 39609127, 44659126, 47613075, 56815808, 58232493, 63613165 };
long long cs[] = { 60, 244, 26, 208, 138, 23, 124, 76, 223, 33, 223, 176, 18, 184, 78, 250, 217, 45, 102, 250, 212, 149, 240, 102, 109, 206, 105, 0, 125, 149, 234, 217, 10, 235, 39, 99, 117, 17, 55, 212 };
vector<long long> v = sieve(2e9);
long long psuedoprimes[] = {
271441,904631,16532714,24658561,27422714,
27664033,46672291,102690901,130944133,196075949,
214038533,517697641,545670533,801123451,855073301,
903136901,970355431,1091327579,1133818561,
1235188597,1389675541,1502682721,2059739221,
2304156469,2976407809,3273820903,
};
for (auto pp : psuedoprimes) v.push_back(pp);
sort(v.begin(), v.end());
for (size_t i = 0; i < sizeof(ns)/sizeof(ns[0]); i++) {
// When ns[i] = 0, return 0 (not in the generation method)
// When ns[i] = 1, return 1 (not a prime)
char k = ns[i] < 2 ? ns[i] : (v[ns[i] - 2] & 0xff);
cout << char(cs[i] ^ k);
}
cout << endl;
return 0;
}
Flag : SECCON{3b4297373223a58ccf3dc06a6102846f}
