Three Trials [RE]

March 2, 2021 5 minute read

Simple reversing challenge with some math. First RE challenge from DSO-NUS 2021.

Challenge Description

Reverse the binary, understand the conditions, dust out your math textbooks and solve the trials!

Files (Any of the links are fine):
https://nusdsoctf2.s3-ap-southeast-1.amazonaws.com/S3/Three_trials/three_trials
https://nusdsoctf.s3-ap-southeast-1.amazonaws.com/S3/Three_trials/three_trials

 >> Flag format conversion may have to be done for this challenge (Refer to notifications)

Solution

The program expects 3 numbers as the input, and then runs three functions to check each of them.

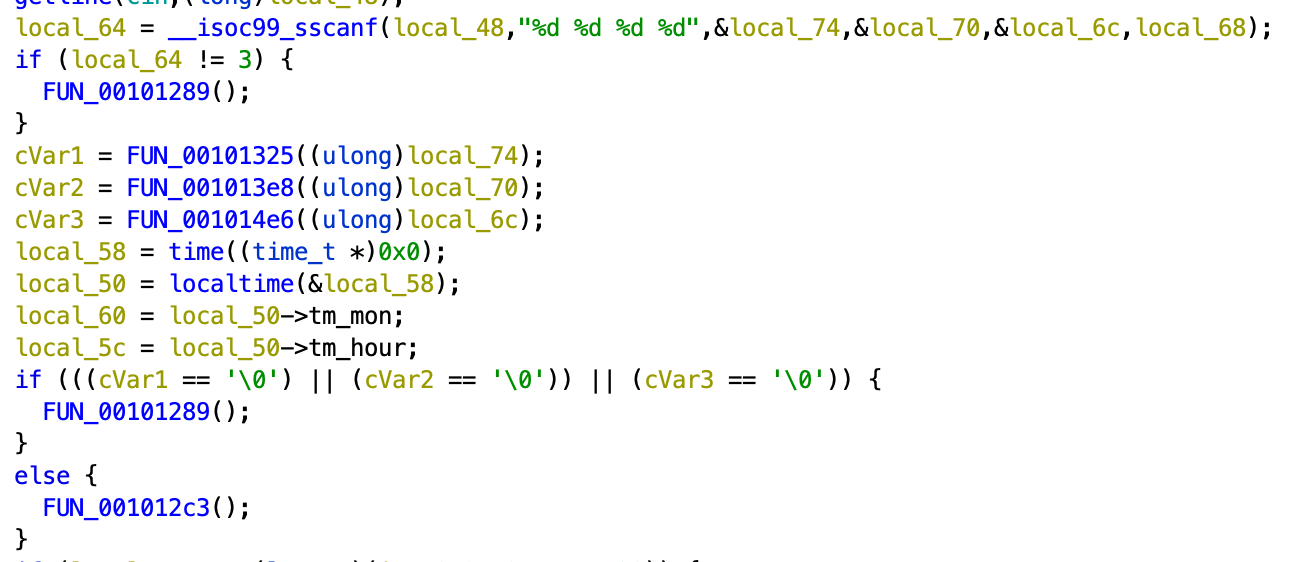
Our goal is to get to the function in the else statement, which means the values of cVar1, cVar2, cVar3 must be non 0.

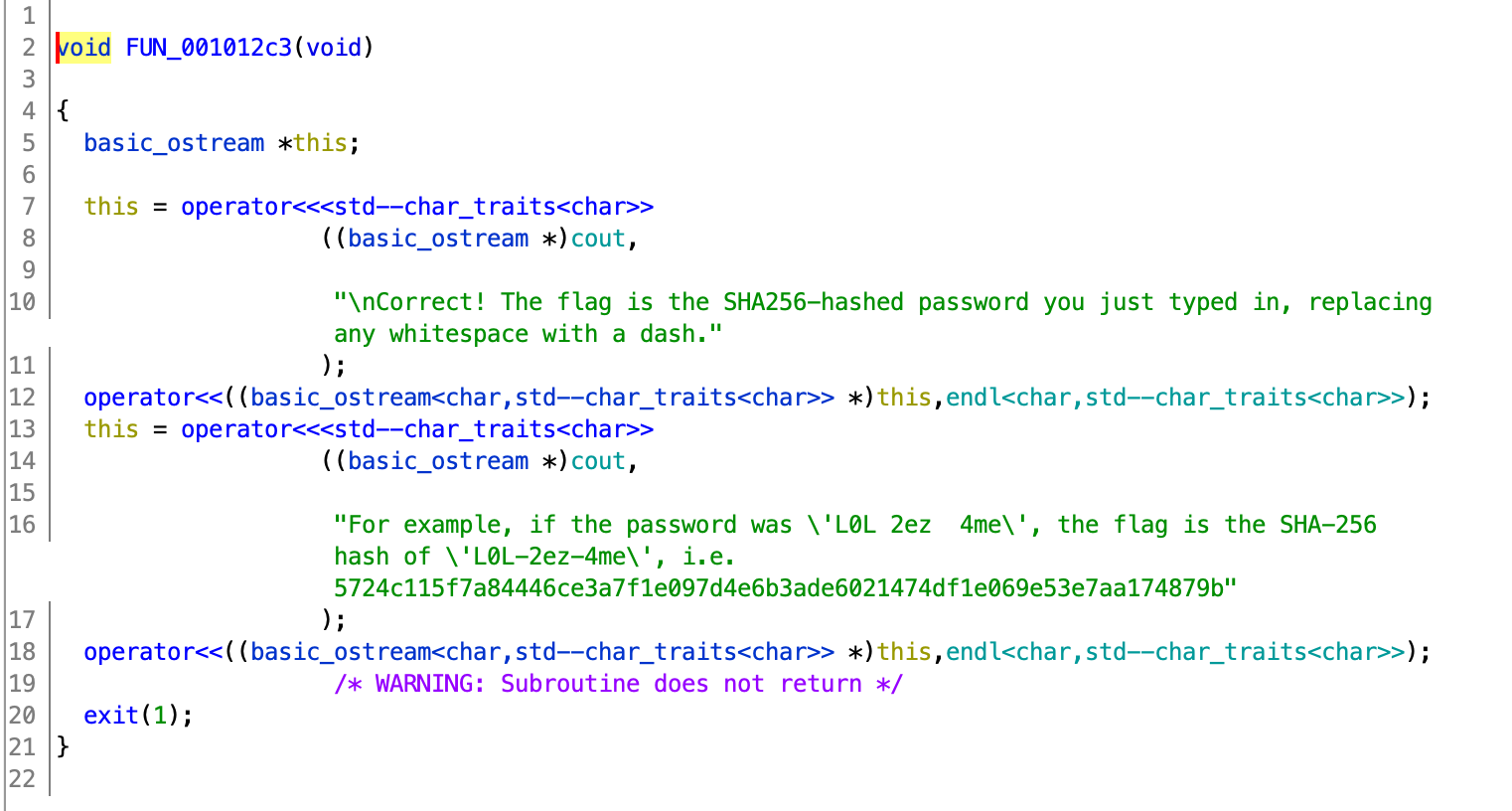
The function in the else statement above

So we’ll just need to reverse the three functions! Easy, right? XD

First trial

local_14 = 0;
local_10 = param_1;
while (0 < local_10) {
  dVar2 = (double)FUN_0010173c((ulong)(uint)(local_10 % 10),3);
  local_14 = (int)(dVar2 + (double)local_14);
  local_10 = local_10 / 10;
}
if (((local_14 == param_1) && (400 < param_1)) && (param_1 < 1000)) {
  uVar1 = 1;
}
else {
  uVar1 = 0;
}
return uVar1;

We want this to return 1. It should be quite obvious that it wants the sum of cube of digits of the argument to be equal to the argument itself.

An example:

$\text{sum of cube of digits of } 123 = 1^3 + 2^3 + 3^3 = 36$

Also, we know that our input is between 400 and 1000, so we can easily write a brute force for that. Solution in python:

for i in range(401, 1000):
    res = 0
    tmp = i
    while tmp > 0:
        res += (tmp%10)**3
        tmp //= 10
    if i == res:
        print(i)
        return

Second trial

dVar3 = (double)FUN_0010173c((ulong)param_1,2); // this directly calls the C function pow()
iVar1 = (int)dVar3;
local_20 = 0;
dVar3 = (double)FUN_0010173c((ulong)param_1,2); // so this is the same as pow(param_1, 2) too
local_1c = (int)dVar3;
while (0 < local_1c) {
  local_20 = local_20 + 1;
  local_1c = local_1c / 10;
}
if ((local_20 - (local_20 >> 0x1f) & 1U) + (local_20 >> 0x1f) != 1) {
  local_18 = 1;
  while ((int)local_18 < local_20) {
    dVar3 = (double)FUN_0010173c(10,(ulong)local_18);
    if (iVar1 % (int)dVar3 + iVar1 / (int)dVar3 == param_1) {
      uVar2 = FUN_0010173c(10,9); // pow(10, 9)
      return uVar2 & 0xffffffffffffff00 | (ulong)(extraout_XMM0_Qa < (double)iVar1);
    }
    local_18 = local_18 + 1;
  }
}
return 0;

local_20 is the number of digits in param_1 squared (notice the pow(param_1, 2)), so local_20 >> 0x1f will always be 0 since our input is only an int. So the if statement is basically

if (local_20 != 1) { ...

So our input is at least 4, since 3*3 == 9 which is a single digit number. Then inside the while loop, it is basically checking whether a given input n has

$n^2 \% 10^k + n^2 / 10^k == n$

for some valid k. Notice that n*n should be greater than 1e9 as seen from the return statement inside the while loop. So this is another easy brute force:

for i in range(4, 2**31):
    if i*i <= 10**9: continue
    if i*i >= 2**31: break

    dig = 0
    sq = i*i
    while sq > 0:
        dig += 1
        sq //= 10

    sq = i*i
    for j in range(1, dig):
        if sq%(10**j) + sq//(10**j) == i:
            print(i)
            return

Third trial

local_10 = 0;
local_c = 1;
while (local_c <= param_1) {
  if ((param_1 % local_c == 0) && (local_c != param_1)) {
    local_10 = local_10 + local_c;
  }
  local_c = local_c + 1;
}
if (((local_10 == param_1) && (dVar1 = (double)FUN_0010173c(10,5), dVar1 < (double)local_10)) &&
   (dVar1 = (double)FUN_0010173c(10,8), (double)local_10 < dVar1)) {
  return 1;
}
return 0;

One sentence to summarize this: A number between 1e5 and 1e8, where the sum of its proper divisors is equal to itself.

A normal brute force will not work as the complexity will be O(n√n), and for n = 1e8, this will take too long to complete. Luckily I found this that proposes a solution of complexity O(n log log n).

result = sum_divisors(10**8)
for i in range(10**5 + 1, 10**8):
    if result[i]-i == i:
        print(i)
        return

Using the sum_divisors function from the link above.

Final Script

def cond1():
    for i in range(401, 1000):
        res = 0
        tmp = i
        while tmp > 0:
            res += (tmp%10)**3
            tmp //= 10
        if i == res:
            print(i, end='-')
            return

def cond2():
    for i in range(4, 2**31):
        if i*i <= 10**9: continue
        if i*i >= 2**31: break

        dig = 0
        sq = i*i
        while sq > 0:
            dig += 1
            sq //= 10
        sq = i*i
        for j in range(1, dig):
            if sq%(10**j) + sq//(10**j) == i:
                print(i, end='-')
                return

def cond3():
    result = sum_divisors(10**8)
    for i in range(10**5 + 1, 10**8):
        if result[i]-i == i:
            print(i)
            return

def sum_divisors(n):
    result = [1] * n
    result[0] = 0
    for p in range(2, n):
        if result[p] == 1: # p is prime
            p_power, last_m = p, 1
            while p_power < n:
                m = last_m + p_power
                for i in range(p_power, n, p_power):
                    result[i] //= last_m    # (B)
                    result[i] *= m          # (B)
                last_m = m
                p_power *= p
    return result

cond1()
cond2()
cond3()

This code takes around 5 minutes or so to run.

Output

407-38962-33550336

Then, we put 407-38962-33550336 into SHA256 and we get our flag!

Flag: DSO-NUS{5137e2ead70710512aa82dfca8727c4eb6803637143a9c2f0c7596ab00352a69}

David Tan